How To simplify rational expressions step-by-step Using algebra 2 help

Wiki Article

The Comprehensive Protection of Algebra 2 Tutoring: Secret Concepts and Skills for Proficiency

Algebra 2 tutoring provides a wide spectrum of important concepts and skills essential for trainees to achieve mastery in mathematics. This encompasses an extensive understanding of polynomial functions, complex numbers, and logarithmic formulas, among others. Each topic constructs on the previous one, creating a cohesive structure for analytic. The application of these ideas in real-world circumstances highlights their relevance. Yet, there stay important areas that can even more enhance a trainee's mathematical journey.

Understanding Polynomial Features

How do polynomial functions form the landscape of algebra? These basic expressions, being composed of variables elevated to non-negative integer powers, offer as the backbone of many algebraic principles. They can be defined by their degree, which shows the highest power of the variable, and their coefficients, which figure out the feature's behavior. Polynomial functions exhibit distinct buildings, such as connection and smoothness, enabling them to design a variety of real-world circumstances. Their visual depictions feature contours that can show various actions, consisting of intercepts and turning points. Recognizing polynomial features involves grasping operations such as addition, department, reduction, and multiplication, along with factoring methods. This fundamental expertise is important for solving inequalities and equations. By realizing polynomial features, pupils create critical problem-solving skills and acquire understanding into more complex mathematical principles, leading the way for advanced researches in algebra and beyond.

Understanding Complex Numbers

Grasping complicated numbers is necessary for pupils in Algebra 2, as these numbers extend the genuine number system to solve formulas that do not have genuine options. Recognizing their interpretation and buildings prepares for doing operations with complicated numbers effectively. This fundamental knowledge will certainly enable students to take on advanced mathematical principles with confidence.

Meaning and Properties

Complicated numbers, a keystone of advanced algebra, extend the principle of one-dimensional number lines to a two-dimensional airplane. Defined as varieties of the type (a + bi ), where (a) and (b) are real numbers and (i) stands for the imaginary unit with the residential or commercial property (i ^ 2 = -1 ), these numbers have one-of-a-kind buildings. The genuine part (a) indicates the horizontal axis, while the imaginary part (b) suggests the vertical axis in the complex airplane. Key properties include their capacity to represent services to polynomial equations that lack real options and their closure under enhancement, multiplication, division, and reduction (except by zero) This structure allows for a deeper understanding of mathematical principles and applications throughout different fields.

Procedures With Complex Numbers

Procedures with complicated numbers create a crucial element of algebra that enhances mathematical understanding and analytical capabilities. Intricate numbers, expressed in the kind (a + bi), where (a) and (b) are real numbers, need certain procedures like addition, division, subtraction, and multiplication.

Enhancement and reduction include integrating like terms, while multiplication uses the distributive residential or commercial property and the fact that (i ^ 2 = -1) Division of complicated numbers necessitates multiplying the numerator and denominator by the conjugate to get rid of the imaginary component in the denominator. algebra 2 help.

These operations not just reinforce fundamental algebra abilities yet also prepare pupils for advanced topics, such as quadratic features and polynomial equations. Proficiency of intricate number procedures outfits learners with critical logical tools.

Checking Out Logarithmic Equations

In the study of logarithmic equations, recognizing the properties of logarithms is important for reliable analytic. These properties offer the fundamental devices required to control and simplify logarithmic expressions. By understanding these concepts, pupils can confidently deal with a range of logarithmic formulas.

Recognizing Logarithm Qualities

Logarithm homes play a crucial role in simplifying and addressing logarithmic equations, using an organized strategy to understanding their habits. These residential properties consist of the power, ratio, and item policies. The item rule states that the logarithm of a product is the sum of the logarithms of its aspects. Conversely, the quotient rule shows that the logarithm of a quotient is the difference of the logarithms. The power rule discloses that the logarithm of a number raised to a backer can be revealed as the backer increased by the logarithm of the base. Proficiency of these homes boosts one's ability to control logarithmic expressions, providing a foundation for dealing with much more intricate equations and features come across in innovative algebra.

Resolving Logarithmic Formulas

Just how can one successfully solve logarithmic formulas? To deal with these equations, it is important to make use of residential or commercial properties of logarithms. Initially, one ought to combine logarithmic expressions making use of the product, power, and ratio policies. This simplification typically changes the formula right into an extra manageable type. Next, transforming logarithmic equations to their rapid form can reveal the unidentified variable. The formula (log_b(x) = y) translates to (x = b ^ y ) In addition, examining services is vital to guarantee they do not produce supplementary results, particularly when handling logarithms. By systematically applying these techniques, individuals can confidently navigate and address logarithmic formulas, enhancing their general understanding and mastery of this mathematical concept.

Analyzing Sequences and Collection

Although series recommended you read and collection might initially appear facility, they are basic principles in algebra that reveal patterns and relationships within numbers. A series is a list of numbers prepared in a specific order, usually defined by a formula or policy. Recognizing the sorts of sequences, such as arithmetic and geometric sequences, enables pupils to recognize the underlying patterns properly.

On the various other hand, a collection is the amount of the regards to a sequence. Evaluating collection includes identifying limitless and finite series, in addition to determining their sums when appropriate. Trainees discover essential techniques, such as using solutions for the sum of arithmetic and geometric series, which streamline estimations.

Understanding sequences and series gears up pupils with vital analytical abilities, allowing them to deal with a lot more complicated mathematical concepts. This structure is essential for their proceeded success in algebra and higher-level mathematics.

Solving Reasonable Expressions and Equations

Rational expressions and formulas stand for vital parts of algebra, involving portions where the numerator and denominator are polynomials. Understanding the resolving of these expressions needs comprehending just how to adjust them successfully. This consists of streamlining expressions by factoring, canceling typical factors, and finding a common measure when including or deducting sensible expressions.

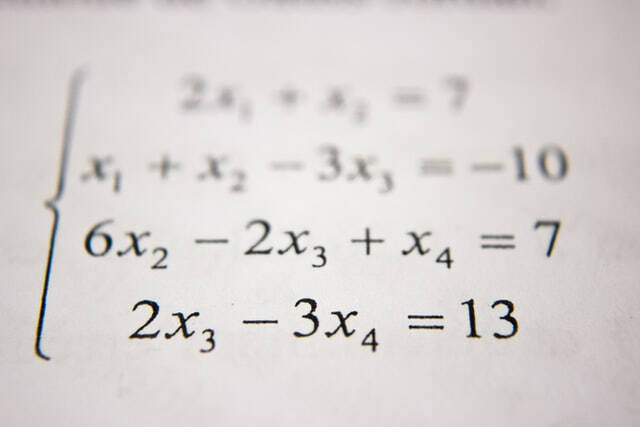
When fixing logical formulas, one need to separate the variable, often by cross-multiplying to get rid of the portions. It is crucial to look for peripheral services, as increasing both sides can introduce values that do not please the initial formula. Furthermore, pupils must recognize restrictions on the variable, as specific values can make the denominator no, rendering the expression undefined.

Understanding Conic Sections

Conic areas are geometric figures derived from the intersection of an airplane and a dual cone. These sections consist of circles, ellipses, parabolas, and hyperbolas, each identified by one-of-a-kind homes and formulas. Recognizing conic areas is essential for students as they discover the partnerships between algebra and geometry.

Circles are defined by a consistent range from a center point, while ellipses result from an aircraft puncturing both cones, developing a shut curve. Parabolas occur from an airplane alongside the axis of the cone, portraying a U-shaped chart. Hyperbolas, on the other hand, take place when the plane intersects both cuts in half of the cone, leading to two distinct, open curves.

In Algebra 2, grasping conic sections entails recognizing their conventional equations, graphing them accurately, and recognizing their crucial features, such as vertices, axes, and foci. This foundational understanding prepares pupils for more sophisticated mathematical ideas.

Using Charts and functions

Features and graphs function as basic tools in Algebra 2, allowing students to model partnerships in between variables and envision mathematical concepts. Proficiency of these components permits students to interpret data, recognize trends, and make forecasts based upon established patterns. Pupils discover different kinds of features, consisting of direct, quadratic, polynomial, rational, and exponential, each with distinct attributes and applications.

Graphing these features includes understanding crucial features such as asymptotes, slopes, and intercepts, which give understandings into their behavior. In addition, students learn to change functions with stretches, changes, and representations, improving their ability to manipulate and evaluate graphical depictions.

Applying functions in real-world contexts further solidifies understanding, as students tackle issues including profit margins, populace development, and read physics equations. This sensible application bridges academic understanding with substantial outcomes, fostering a deeper admiration for the relevance of functions and graphs in day-to-day life.

Frequently Asked Inquiries

Exactly How Can I Boost My Problem-Solving Abilities in Algebra 2?

To boost analytic skills in Algebra 2, one must exercise on a regular basis, seek varied troubles, use on-line resources, collaborate with peers, and concentrate on understanding underlying ideas as opposed to memorizing procedures, promoting deeper understanding and application.

What Resources Are Recommended for Added Algebra 2 Method?

Advised resources for extra Algebra 2 practice include online platforms like Khan Academy, textbooks with technique issues, and tutoring solutions. Involving in math discussion forums can also give diverse analytic methods and get more collaborative knowing opportunities.

Are There Online Tutoring Options Available for Algebra 2?

Yes, many on-line tutoring options exist for Algebra 2 (algebra 2 help). Platforms like Khan Academy, Chegg Tutors, and Wyzant deal customized assistance, video lessons, and interactive workouts, dealing with numerous finding out designs and timetables for pupils looking for assistance

Exactly how Do I Plan for Algebra 2 Tests Properly?

To prepare properly for Algebra 2 exams, one should review crucial principles, method issues routinely, use on the internet resources, create research groups, and take method tests to recognize staminas and weaknesses for targeted improvement.

What Prevail Misunderstandings Students Have in Algebra 2?

Students frequently misinterpret the relevance of fundamental ideas, thinking they can miss prerequisites. They might likewise fight with abstract reasoning, confusing features with formulas, and misinterpreting the role of variables in algebraic expressions.

Understanding intricate numbers is important for students in Algebra 2, as these numbers expand the actual number system to address formulas that do not have genuine options. These operations not just strengthen fundamental algebra abilities however additionally prepare students for more innovative subjects, such as quadratic functions and polynomial equations. Reasonable expressions and equations represent vital parts of algebra, including portions where the numerator and are polynomials. In Algebra 2, mastering conic areas involves identifying their common formulas, graphing them properly, and recognizing their crucial features, such as emphases, axes, and vertices. Using features in real-world contexts better solidifies understanding, as pupils deal with troubles entailing revenue margins, population growth, and physics equations.

Report this wiki page